前面一篇的面试题主要考察一些小trick,见过了就很容易,没见过的话可能就很难。今天介绍一类问题,也是经常作为训练的题目。给定整数数组A[1…n],判断是否可以从中选出若干个数,使它们的和恰好为K。比如A[]={1,2,4,7},K=13。应该返回2,4,7。
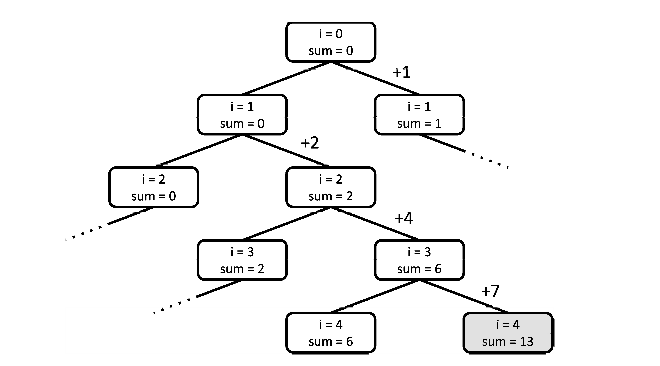
先介绍一种简单的方法:状态搜索,对于数组A[]中的元素只有两种可能:选或者不选。所以我们可以得到下面这张图,然后对这张图进行搜索就可以了。思想很简单,代码写起来就是深度优先搜索和广度优先搜索那一套,代码实现起来也比较模式化,注意下边界条件就可以。下面的代码输入以vector代表数组,实现也比较简单。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
| vector<vector<int> > ret;
void DFS(vector<int>& candidates, vector<int> elements, int target, int pos)
{
if(target == 0)
{
ret.push_back(elements);
return;
}
if(pos==candidates.size() || target<0)
return;
DFS(candidates, elements, target, pos+1);
elements.push_back(candidates[pos]);
DFS(candidates, elements, target-candidates[pos], pos+1);
elements.pop_back();
}
vector<vector<int> > combinationSum(vector<int>& candidates, int target){
vector<int> elements;
DFS(candidates, elements, target, 0);
return ret;
}
|
但是这个代码是不是没有问题了呢?考虑一种情况A[]={1,1,6,1}, K=8。则上面的代码返回{1,1,6}, {1,6,1}, {1,6,1},不要问为什么,人工测试一下就明白了。下面对代码进行了一点优化。现在比较流行微创新,其实一点点小的改进往往是程序中最关键的地方。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
| vector<vector<int> > ret;
void DFS(vector<int> &candidates, vector<int> elements, int target, int pos)
{
if(target == 0)
{
ret.push_back(elements);
return;
}
if(pos==candidates.size() || target<0)
return;
int same=1;
for(size_t i=pos+1; i<candidates.size() && candidates[pos]==candidates[i]; i++,same++)
;
for(int i=0; i<same; i++)
{
for(int j=0; j<i; j++)
elements.push_back(candidates[pos]);
DFS(candidates, elements, target-candidates[pos]*i, pos+same);
for(int j=0; j<i; j++)
elements.pop_back();
}
}
vector<vector<int> > combinationSum(vector<int>& candidates, int target){
vector<int> elements;
sort(candidates.begin(), candidates.end());
DFS(candidates, elements, target, 0);
return ret;
}
|
好了,下面看上面问题的一个变体:给定整数数组,元素各不相同,并且每个元素使用多次,其他条件和要求不变。仿照上面的代码框架很快就可以写出下面的代码来了。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
| vector<vector<int> > ret;
void DFS(vector<int> &;candidates, vector<int> elements, int target, int pos)
{
if(target == 0)
{
ret.push_back(elements);
return;
}
if(pos==candidates.size())
return;
for(int i=0; candidates[pos]*i<=target; i++)
{
for(int j=0; j<i; j++)
elements.push_back(candidates[pos]);
DFS(candidates, elements, target-candidates[pos]*i, pos+1);
for(int j=0; j<i; j++)
elements.pop_back();
}
}
vector<vector<int> > combinationSum(vector<int>& candidates, int target){
vector<int> elements;
sort(candidates.begin(), candidates.end());
DFS(candidates, elements, target, 0);
return ret;
}
|
仔细分析一下上面的问题,如果数组大小为N,那么状态数就是2^N,复杂度高达O(2^N)。搜索我们基本可以不考虑了。这时候另外一种重要的方法开始登场了,对,就是动态规划,关于动态规划,这里就不介绍了。我们这里只针对具体的问题,从问题中分析出不变的东西。废话不多说,下面如何分析这个问题。为了方便的分析问题,集中到核心问题上来,我们不要求返回具体元素,只需要返回true或false。这里假定大家都了解了动态规划的基本的知识,如果不清楚,建议学习《算法导论》上关于动态规划的讲解。动态规划中,最重要的是最优子结构的证明和状态转移方程的推导。最优子结构的意思是局部最优解能决定全局最优解(对有些问题这个要求并不能完全满足,故有时需要引入一定的近似)。简单地说,问题能够分解成子问题来解决。对于本题,我们作如下定义:dp[i+1][j]==(数组A[0…i]可以表示出j?)。也就是说如果能表示,则为true,否则为false。所以题目等价于求dp[n+1][K],而dp[n+1][K]的求解取决于dp[n][K]和dp[n][K-A[n]],这样就分解成子问题。状态转移方程也很简单:dp[i+1][j]=dp[i][j]|dp[i][j-A[i]]。最后还有一点要注意的是初始化!
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
| bool combinationSum(int A[], int n, int K){
bool **dp = new bool* [n+1];
for(int i=0; i<=n; i++)
dp[i] = new bool [K+1];
for(int i=0; i<=n; i++)
dp[i][0] = true;
for(int i=0; i<=n; i++)
{
for(int j=1; j<=K; j++)
dp[i][j] = false;
}
for(int i=1; i<=n; i++)
{
for(int j=1; j<=K; j++){
dp[i][j] = j-A[i-1]>0 ? (dp[i-1][j]|dp[i-1][j-A[i-1]]) : dp[i-1][j];
}
}
bool ret = dp[n][K];
for(int i=0; i<n; i++)
delete [] dp[i];
delete [] dp;
return ret;
}
|
最近感觉坚持这种小事,很少有人可以做到。如果你可以坚持下来,你在无形中已经打败了很多人了。最简单的坚持,最后的结果也是惊人的!
